Vision Transformer with Quadrangle Attention
作者信息

一句话总结
摘要
基于窗口的注意力很好用,但是手动设计窗口的参数与输入数据无关,这限制了 Transformer 对不同物体,大小、形状、和方向等属性的感知能力。
因此提出了四边形注意力 QA,将基于窗口的注意力扩展到四边形公式中。提出端到端的四边形回归模块,将预测框框变换成预测四边形的 Koken。提出了一个框架,在分类,检测,语义分割,姿态识别等任务上表现良好。
动机(介绍和相关工作)
现有方法遇到的问题
ViT 在视觉任务中很有效,它把输入的图像切成小块并编码,然后把二维图像视为一维序列,使用多头注意力和 FFN 处理。但是原始的注意力计算 Attention Map 的复杂度是 $o(n^2)$,这导致 Transformer 在处理高分辨率图像是十分困难的。因此局部窗口的 Transformer 将图像划分为几个正方形的窗口,在每个窗口内使用注意力,平衡了性能与资源。这种方法对窗口进行了约束,限制了 Transformer 的长程建模能力和对不同对象的大小,形状和方向的感知,然而这些属性在视觉任务中十分重要。
现有的方法是怎么做的,为什么这样做不好
以前的研究侧重于设计高级的结构,使得可以更好的进行长程建模,以改进基于窗口的注意力。Swim 使用大的滑动窗口(7->32),Focal attention 使用 coarse granularity tokens 捕获长程信息,cross-shaped window attention 使用相互垂直的矩形窗口捕获水平和垂直方向的信息,Pale 从水平垂直和对角方向建立长程依赖关系。这些方法通过增加注意力的距离提升分类的性能。尽管图像中目标的大小、形状和方向都是任意的,但是这些方法都采用了固定的矩形窗口进行计算。这种与数据无关的窗口设计对于 ViT 来说可能是次优的。
作者是怎么做的。
在这篇研究中,作者提出了一个数据驱动的解决方案,将矩形拓展到四边形,其中的形状大小和方向都是可以自动学习的。它能使 Transformer 更好的学习到不同的特征,用于表示不同的对象。
提出了新的注意力方法,从数据中学习物体的四边形配置,计算局部注意力。使用默认的窗口对图像进行分区,之后使用端到端的可学习四边形回归模块预测每个窗口变化,将默认窗口转换为目标四边形。
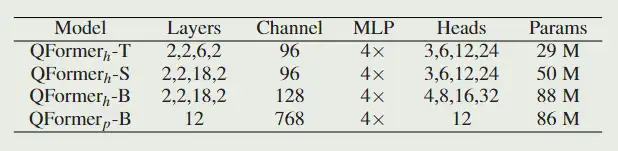
具体来说,作者提出了一种新的注意方法 Quadrangle Attention (QA),用于学习自适应四边形参数,以计算局部注意。它使用默认窗口对输入图像进行分区,并使用端到端可学习的四边形回归模块来预测每个窗口的参数化变换矩阵。变换包括平移、缩放、旋转、剪切和投影,用于将默认窗口转换为目标四边形。为了提高训练的稳定性并允许良好的可解释性,变换矩阵被表述为几个基本变换的组合。与窗口注意不同,在多头自注意(MHSA)层中不同头部之间共享窗口定义不同,所提出的四边形变换对每个头部独立执行。这种设计使注意力层能够对不同的长期依赖关系进行建模,并促进重叠窗口之间的信息交换,而不需要窗口移位 或 Token 置换。作者提出了 QFormer 架构,在许多任务上都取得了优异的成绩。
主要贡献有三点:
- 提出了一种新的四边形注意力方法
- 提出了 QFormer 的新架构
- 实验表明提出了架构在各个代表性的任务上取得了优秀的表现
方法
四边形注意力
基本窗口生成
首先将特征图划分为几个预设大小的窗口
四边生成
定义如下变换矩阵 T: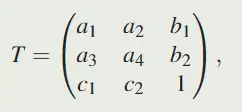 ,a = [a1, a2;a3, a4]定义了缩放、旋转和剪切的转换,b = [b1;b2]定义了平移,c = [c1, c2]是一个投影向量,它定义了当观察者的视角在深度维度上变化时感知对象如何变化。
,a = [a1, a2;a3, a4]定义了缩放、旋转和剪切的转换,b = [b1;b2]定义了平移,c = [c1, c2]是一个投影向量,它定义了当观察者的视角在深度维度上变化时感知对象如何变化。
直接回归八个参数并不容易,因此将其拆分。首先预测 $t \in R^9$,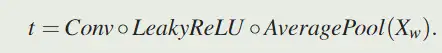
得到 t 后,根据如下公式得到对应的参数: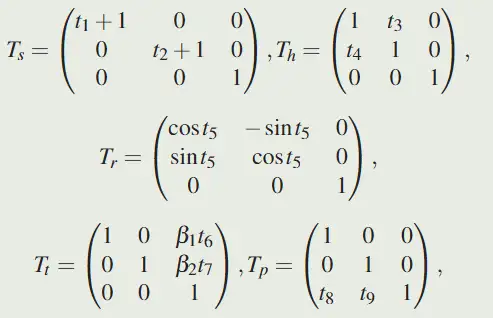 ,其中 $\beta_1=\frac{W}{w}, \beta_2=\frac{H}{h}$ 是缩放相关的参数,以帮助使模型适应不同的输入大小
,其中 $\beta_1=\frac{W}{w}, \beta_2=\frac{H}{h}$ 是缩放相关的参数,以帮助使模型适应不同的输入大小
最终的 T 计算如下: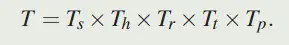
给定点 $(x_1, y_1)$,根据如下计算就能得到变换点的坐标:
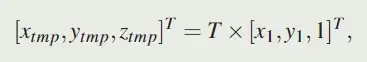
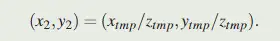
投影的过程具体如下图所示:

两个不同参数的变换,在绝对坐标系下的对比如下:
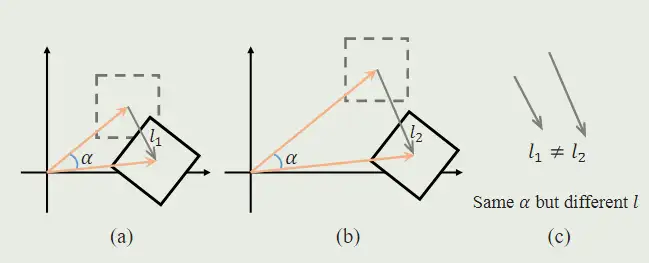
当 $t=0$ 时,变换后的四边形就是原始的窗口。初始化时,t 都会初始化成 0.
在同一坐标下使用坐标变换可能会导致歧义。 如图所示,a 的原点更靠近坐标中心。经过它们都有相同的投影变换矩阵,但是变换前后的差别非常大。因此变换是基于每个窗口的相对坐标来进行的,而不是基于绝对坐标。
如图所示,a 的原点更靠近坐标中心。经过它们都有相同的投影变换矩阵,但是变换前后的差别非常大。因此变换是基于每个窗口的相对坐标来进行的,而不是基于绝对坐标。
,其中 $x^c, y^c$ 是窗口中心点的坐标,通过变换得到相对坐标,然后使用四边形注意力处理,得到 $x_r^q, y_r^q$,然后在使用如下公式变换回去
获得坐标后,使用网格采样对 Key 和 Value 进行采样,得到 $K_w, V_w $
四边形的区域可能重叠,但是也可能产生覆盖特征图外区域的四边形,因此对超过特征图的区域填充 0,最终使用 $K_w, V_w $ 和原始的 $Q_w $ 计算
正则化
由于有区域可能在特征图之外,这些区域的梯度总是 0,这阻碍了四边形回归模块的学习,因此设计了一个正则化项来鼓励投影四边形覆盖有效区域
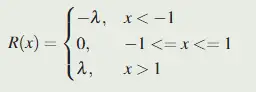
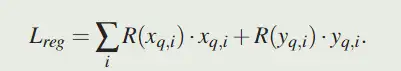 ,其中 λ 是超参数
,其中 λ 是超参数
模型规模